ऑपरेटर्स और एक्सप्रेशंस

Operators and Expressions

Operators

Operators are special symbols that are used for computations in Python. The operators .require operands which can be variables and/or constants to work on. An example of an operator would be +. An expression is a combination of an operator and its operands; for example. 4+5. The operators in Python can be categorized as : Arithmetic, Relational, Logical, assignment and Identity operators.

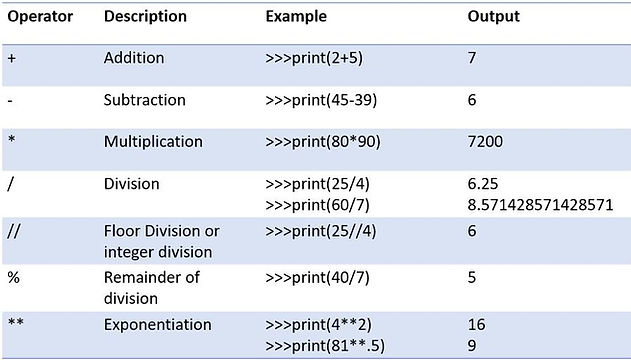
Arithmetic Operators

These operators work on numeric values . The operators can be further categorized according to the number of operands they require. Unary operators work on a single operand whereas binary works on two operands. Let us examine each one in detail.

Using Arithmetic operators with Strings

The arithmetic operators + and * can also be used with strings. The following code illustrates this:

Using +

>>> "Hello" +"Python"
'HelloPython'
>>> x="Good"
>>> y="Morning"
>>> x+y
'GoodMorning'

Using *

>>> "Ball" * 2
'BallBall'
>>> y="Frog"
>>> y*4
'FrogFrogFrogFrog'

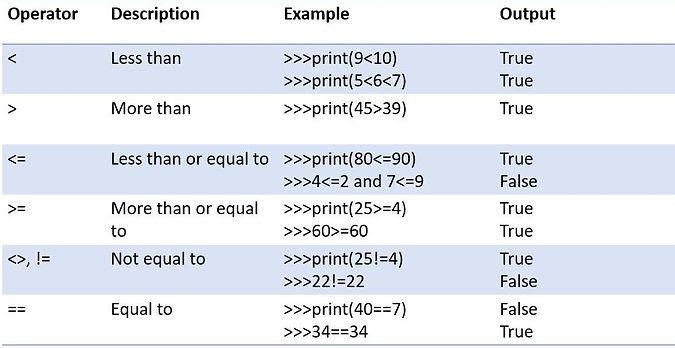
Relational operators

These are also known as relational operators. When applied they return a value True or False.

Examples of relational operators in use:

>>> 60>90
False
>>> 99<200
True
>>> a=45
>>> b=34
>>> a>b
True
>>> a<b
False
>>> a==b
False
>>> a!=b
True
>>> x=90
>>> y=90
>>> x>=y
True
>>> x=99
>>> x>=y
True

We can use relational operators with strings also. When we use them with strings , the strings are compared from left to right, using the ASCII values of the characters. The strings are always compared in a lexicographical manner i.e. according to their appearance in the dictionary.

For example:

>>>"Hello"<"hello"

True

This is because the ASCII code of 'H' is 65 and that of 'h' is 104. Therefore "Hello" is smaller than "hello"

>>> "yearly"<"monthly"
False

Logical Operators

These operators are used to join expressions containing arithmetic and /or relational operators to form complex expressions. There are three logical operators and, or and not. Consider the following table. Here x and y are two expressions.

Using not in code

>>> x=99
>>> y=89
>>> z=90
>>> not x>80
False
>>> not y<80
True

Using and

>>> x=99
>>> y=89
>>> z=90
>>> x>y and z>60
True
>>> x>z and y!=z
True
>>> z<x and y>=40
True
>>> z<x and y>x
False

Using or

>>> x=99
>>> y=89
>>> z=90
>>> x<y or x!=80
True
>>> x==99 or z<80
True
>>> y>z or x>y
True
>>> x<y or z<y
False

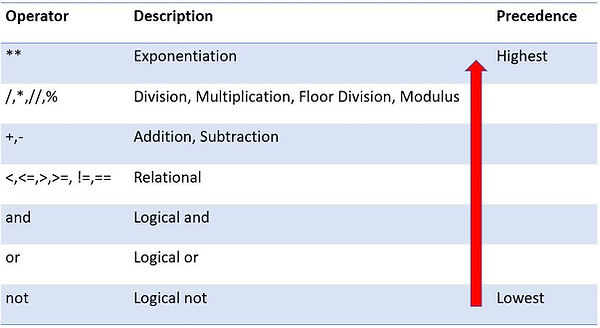
Operator precedence

When we have expressions with more than one operator, it becomes ambiguous as to which operation to perform first, which to perform second and so on. Therefore every language assigns a precedence to all the operators that are supported.

So therefore in an expression, an operators of highest precedence are applied first. Operators of the next highest precedence are performed and so on till the expression is fully evaluated. Any operators of equal precedence are performed in left-to-right order.

Python assigns the following precedence to various operators:

In the above table the operators are arranged in descending order of precedence with exponentiation having highest precedence and logical or having lowest precedence. The operators having same precedence are arranged in a single row and they evaluate from left to right.

Example of operator precedence:

>>> 4+5*9-2
47
>>> 3**4*2
162

In the first statement, first 5 is multiplied by 9, the product, 45 is added to 4 to obtain the sum, 49. 2 is then subtracted from 49 to give final result 47. Similarly in the second statement 3 is first raised to power 4 and the result is multiplied by 2.

Sometimes we need to override operator precedence. We can use brackets to do this.

>>> (4+5)*9-2
79
>>> 3**(4+2)
729

The operation in the brackets are always performed first. Therefore in the first statement, the parenthesized expression, (4+5) is evaluated first (4+5=9), which is multiplied by 9 (9*9=81), and finally 2 is subtracted from the result(81-2=79.

We can use any number of brackets in an expression.

Python shorthand/Augmented Assignment Operators

When using arithmetic operators, it is common to update the value of a variable. For example if we wish to increase the value of a variable x by 2, we would write the following:

>>>x=4

>>>x=x+2

>>>x

6

The value of x is 4. When we add 2 to it, the value becomes 6. Note that the variable x is incremented, therefore it is present on both sides of the = (assignment) operator. Python provides shorthand assignment operators which can be used for this purpose. These are:

Hence the above code can be written as :

>>>x=4

>>>x+=2

>>>x

6

Expressions

An expression may consist of a combination of:

variables
constants
operators

An expression needs to be evaluated thus it is usually assigned to a variable or appears in a print statement.

Examples of expressions are:

Expression operands Type Will evaluate to

x+y*2+34 variables, constants arithmetic a numeric value

a>b variables relational a Boolean value

"Great"!="great" string constants relational a Boolean value

a+b > c+d variables mixed a Boolean value

x!=y and z>4 variables, constants mixed a Boolean value

4*(45+60) constants arithmetic a numeric value

The expression may be arithmetic, logical or conditional depending on the operators used. It may be a combination of all.

Using expressions:

>>> a=24+30-9*2
>>> a
36
>>> b=a+20
>>> b
56
>>> a=b>9
>>> a
True
>>> 20+90/8-2
29.25
>>>

Sample Program: Write a program to input two numbers and display the sum, product, quotient and product

The Math module

There are some operations like finding the square root or raising a number to a power. For example to express the following equation in Python, we shall require special functions other than the operators.

x=

The math module in Python contains a collection of mathematical functions which enable such complex mathematical calculations or equations to be expressed. In this section we shall cover only two such functions, math.pow() and math. sqrt(). We shall cover the module in detail in a later unit.

In order to be able to use the functions in the math module we need to first import it using the following statement:

import math

1. math.pow(x,y)

This function returns the value of x raised to the power y.

Example:

>>> import math
>>> print(pow(2,4))
16

>>> import math

>>> print(math.pow(9,2)) #we can also use this method of writing

81

2. math.sqrt(x)

This function returns the square root of the number x. x must be a positive number.

Example:

>>> import math

>>> print(math.sqrt(16)) #the sqrt function requires math to be prefixed to the call

4

The number in the brackets has to be a positive number otherwise an error will be generated.

Example:

>>> import math
>>> print(math.sqrt(-16))
Traceback (most recent call last):
File "<pyshell#1>", line 1, in <module>
print(math.sqrt(-16))
ValueError: math domain error